REFRACCIÓN,
DIFRACCION Y REFLEXIÓN
Cuando la luz incide sobre la superficie de separación de
dos medios que poseen velocidades de luz diferentes, parte de la energía
luminosa se transmite (refracción) y parte se refleja (reflexión).
REFRACCIÓN.
Sólo se produce si
la onda incide oblicuamente sobre la superficie de separación de los dos medios
y si éstos tienen índices de refracción distintos. ◼ El índice de refracción,
n, es un número adimensional que
caracteriza a un medio transparente, y de define por: n=c/v ◼ Donde c es la
velocidad de la luz en el vacío, y v la velocidad de la luz en el medio
Para el agua, n=1.33, mientras que para el vidrio n varía
de 1.50 a 1.66, según sea el tipo de vidrio. El índice de refracción del
diamante es muy elevado, 2.4. ¿Qué significa esto? El del aire es 1,0003.
¿Qué significa esto? Por eso podemos suponer que la velocidad de la luz en el
aire es la misma que en el vacío.
La refracción sólo se produce si la onda incide
oblicuamente sobre la superficie de separación de los dos medios y si éstos
tienen índices de refracción distintos.
La refracción se origina en el cambio de velocidad de
propagación de la onda.
Ley de Snell de la refracción
Fue descubierta experimentalmente por Willebrod Snell en
1621. Y dice que los ángulos de incidencia y refracción vienen relacionados
por: n 1 senθ 1 =n 2 senθ 2
Ejemplo
Un rayo de luz que
se propaga en el aire entra en el agua con un ángulo de incidencia de 45º. Si
el índice de refracción del agua es 1.33, ¿Cuál es el ángulo de refracción?
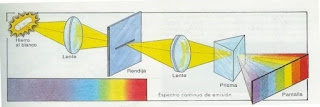
Efectos ópticos debidos a la refracción
Los rayos de luz se desvían (refractan) cuando pasan del
agua al aire, haciendo que los objetos parezcan menos profundos y más cerca del
observador.
La luz es refractada cuando entra en el bloque, y vuelta a
refractar cuando lo deja y vuelve al medio original (saliendo paralela)
La curvatura de la superficie de una lente produce una
refracción que varía con el ángulo de curvatura.
Reflexión de la imagen en un espejo
Para observar el punto B, la luz desde el punto A debe
parecer que viene desde el punto A’, en el espejo.
Reflexión interna total
El prisma permite demostrar la relexión interna total si el
ángulo de incidencia es suficientemente grande.
REFLEXIÓN
Cuando un rayo de luz llega
a una superficie lisa de una placa de vidrio, ocurre que en virtud de que el
vidrio es transparente, parte de esta luz penetra en la lámina, es decir, se
refracta y otra parte vuelve a propagarse en el aire en otra dirección,
experimentando de este modo una reflexión.
En la práctica, ocurre que
la mayoría de los cuerpos refleja difusamente la luz que incide sobre ellos;
así por ejemplo una hoja de papel, una pared, un mueble, una persona, etc., son
objetos que difunden la luz que reciben en todas direcciones, de esta forma la
luz que penetra en nuestros ojos hace que veamos la imagen del objeto
observado.
Elementos
(1) Rayo reflejado: Es el
rayo que rebota (sale) de la superficie P.
(2) Normal: Es la línea (imaginaria) perpendicular a la superficie P.
(3) Ángulo de incidencia (i): Es el ángulo formado entre el rayo incidente y la normal.
(4) Ángulo de reflexión (r): Es el ángulo formado entre el rayo reflejado y la normal.
(2) Normal: Es la línea (imaginaria) perpendicular a la superficie P.
(3) Ángulo de incidencia (i): Es el ángulo formado entre el rayo incidente y la normal.
(4) Ángulo de reflexión (r): Es el ángulo formado entre el rayo reflejado y la normal.
Espejos
planos
Un espejo es toda superficie pulimentada que
refleja perfectamente la luz. La distancia de la imagen al espejo es igual a la
distancia que hay entre el objeto y espejo; por esta razón la imagen tiene el
mismo tamaño del objeto y es simétrica de él en relación con el espejo.
El
rayo marcha perpendicular al frente de las ondas
Cuando un rayo incide sobre
una superficie plana, pulida y lisa y rebota hacia el mismo medio decimos que
se refleja y cumple las llamadas "leyes de la reflexión" :
1.- El rayo incidente forma con la normal un ángulo de incidencia que es igual al ángulo que forma el rayo reflejado con la normal, que se llama ángulo reflejado.
2.- El rayo incidente, el rayo reflejado y la normal están en un mismo plano
La difracción es la desviación que sufren las ondas alrededor
de los bordes que se produce cuando un frente de onda (ya sea sonora, material
o electromagnética) es obstruido por algún obstáculo. No hay una distinción
física significativa entre interferencia y difracción.
El esquema de la onda resultante puede calcularse
considerando cada punto del frente de la onda original como una fuente puntual
de acuerdo con el principio de Huygens y calculando el diagrama de
interferencia que resulta de considerar todas las fuentes. El principio de
Huygens dice que cada punto en el frente de una onda sirve de fuente de onda
esféricas secundarias tales que la forma del frente de onda primario un
instante de tiempo más tarde es la envolvente de esas ondas secundarias. Además
estas ondas secundarias avanzan en cada punto del espacio con una rapidez y
frecuencia igual a la de la onda primaria.
El principio de Huygens no puede explicar el proceso de
difracción. Las ondas de sonido se «doblan» fácilmente alrededor de objetos
grandes como los postes de teléfono y los árboles, los cuales por el contrario
forman sombras muy definidas cuando se iluminan con luz. Sin embargo, el
principio de Huygens es independiente de cualquier consideración de longitud de
onda y predecirá las mismas configuraciones de onda en ambas situaciones.
Esta dificultad fue resuelta por Fresnel con su adición del
concepto de interferencia. El principio de Huygens-Fresnel establece que cada
punto sin obstrucción de un frente de onda, en un instante de tiempo dado,
sirve como una fuente de ondas secundarias esféricas (de la misma frecuencia de
la onda primaria). La amplitud del campo óptico en cualquier punto adelante es
la superposición de todas estas ondas considerando sus amplitudes y fases
relativas.
Cuando se combinan dos ondas armónicas procedentes de dos
focos de la misma frecuencia y longitud pero de diferente fase, la onda
resultante es una onda armónica cuya amplitud depende de la diferencia de fase.
Si la diferencia de fase es cero o un número entero de veces 360º (2p radianes)
las ondas están en fase y la interferencia es constructiva. La amplitud
resultante es igual a la suma de amplitudes individuales y la intensidad (que
es proporcional al cuadrado de la amplitud) es máxima. . Si la diferencia de
fase es 180º (p radianes) o un número entero impar de veces 180º (p radianes)
las ondas están desfasadas y la interferencia es destructiva. En este caso la
amplitud resultante es igual a la diferencia entre las amplitudes individuales
y la intensidad es un
Mínimo. Si las amplitudes individuales son iguales, la
intensidad máxima es cuatro veces la intensidad de cada uno de los focos y la
intensidad mínima es cero. En general, una diferencia de trayectos de Dr
contribuye a una diferencia de fase d dada por:
2 r δπ λ ∆ =
Otra causa de diferencias de fase es el cambio de fase en
180º (p radianes) que sufre una onda cuando se refleja en una superficie límite
determinada en cuyo material la velocidad de la onda es menor. Por ejemplo,
Cuando la luz que se propaga en aire incide sobre la superficie de un medio en
el que la luz se desplaza más lentamente, como un vidrio o el agua, existe un
cambio de fase de 180º en la luz reflejada.
La interferencia de ondas procedentes de dos focos no se
observa a no ser que los focos sean coherentes, es decir, la diferencia de fase
entre las ondas procedentes de los focos debe ser constante con el tiempo. Esto
no es habitual porque normalmente un haz de luz es el resultado de millones de
átomos que irradian independientemente. Habitualmente en óptica se consigue la
coherencia dividiendo, en dos o más haces, el haz de luz procedente un foco.
Los láseres son hoy en día la fuente más importante en el laboratorio de luz
coherente en el laboratorio.
DIFRACCIÓN DE FRESNEL Y DIFRACCIÓN DE FRAUNHOFER.
Consideremos un blindaje opaco, y un frente de ondas
procedente de una fuente puntual
Cuando colocamos una pantalla frente a la ranura podemos
observar dos situaciones límite: − La
pantalla este cercana a la ranura. Se observa una imagen que corresponde a la
Difracción de Campo Cercano o Difracción de Fresnel.
La pantalla esta
alejada de la ranura. Se observa una imagen que corresponde a la Difracción de
Campo Lejano o Difracción de Fraunhofer.
Estos dos fenómenos son manifestaciones de un mismo
proceso, la interferencia. Analizaremos el proceso de campo lejano porque
permite un tratamiento matemático más simple.
Consideremos la difracción de Fraunhofer con una rendija
única de anchura a. Supondremos que se divide en N intervalos la rendija de
anchura a y que existe un foco puntual de ondas en el punto medio de cada
intervalo. Si la distancia entre dos fuentes adyacentes es l y a es la anchura
de la abertura tenemos que /
Como la pantalla está muy alejada, los rayos procedentes de
las fuentes puntuales y que llegan a un punto P de dicha pantalla son
aproximadamente paralelos. La diferencia de los trayectos entre dos fuentes
cualesquiera adyacentes es entonces lsen θ y la diferencia de fases es la amplitud de una sola fuente, la amplitud en
el punto máximo central en donde 0 θ = y todas las ondas están en fase, es máxA
NA = El valor de la intensidad en otro punto cualquiera en un cierto ángulo q
se obtiene sumando las ondas armónicas y se obtiene:
Donde 0 I es la intensidad del punto central que es máxima
y f es la semidiferencia de fase entre la primera y última onda y vale: hacen
Los extremos de I( q ) se presentan para valores que hacen
que dI d φ sea cero, esto es
La función de difracción presenta mínimos en cuando el seno
de f se anula, es decir:
Mientras que los máximos de esta función aparecen a valores
de f donde se vuelve cero la expresión cos 0 sen φ φφ − = o lo que es igual tan
φ φ = , es decir:
Cuando se tienen dos o más rendijas, el diagrama de
intensidad obtenido en una pantalla lejana es una combinación del diagrama de
difracción de una sola rendija y el diagrama de interferencia de varias
rendijas. La intensidad obtenida para este caso es:
Donde 0 I es la intensidad del punto central que es máxima
y f es la semidiferencia de fase entre la primera (parte superior) y última
onda y χ es la semidiferencia de fase entre los rayos que proceden de los
centros de las dos rendijas, que se relaciona con la separación d de las
rendijas por:
Si ahora analizamos la expresión completa, esta puede
considerarse como un término de interferencia, modulado por uno de difracción, Interferencia
difracción
Es posible obtener ahora los máximos y mínimos de ambas
funciones; la función de difracción presenta mínimos en los valores mostrados
anteriormente. En cuanto a la función de interferencia, esta presenta mínimos a
los siguientes valores. Los máximos de la función de interferencia.
Se puede observar que la intensidad puede expresarse por un
término principal de interferencia modulado por el término de difracción.
Cuando existen muchas rendijas equiespaciadas se presentan
los máximos de interferencia en los mismos puntos que cuando había dos
rendijas, pero los máximos son mucho más intensos y mucho más estrechos. En el
caso de n rendijas, la intensidad de los máximos principales es 2 0 nI
(modulado por el término de difracción) y existen n-2 máximos secundarios entre
cada para de máximos principales. En la figura se observan los diferentes
patrones de difracción para una, dos, tres, cuatro y cinco rendijas; en las que
se puede apreciarlos anteriormente dicho.
REDES DE
DIFRACCIÓN.
Es un conjunto repetitivo de elementos difractores de una
onda emergente, bien sean aberturas u obstáculos que producen alteraciones de
la fase, la amplitud o ambas.
Una de las redes más simples es una disposición múltiple de
rendijas. Se atribuye su invención al astrónomo norteamericano David Rittenhouse
en 1785, pero posteriormente fue ampliamente estudiado por Fraunhofer. Existen
varios tipos de dispositivos, entre ellos:
Redes de transmisión en amplitud. Físicamente son rejillas
de alambre fino. Redes de transmisión o reflexión en fase. Se construyen
mediante vidrios con hendiduras.
Las redes bidimensionales están constituidas por
distribuciones de N objetos difractores idénticos cuyo resultado se puede ver
como el de N patrones de Fraunhofer que se superponen.
Si la disposición bidimensional es irregular se obtiene una
intensidad que aumenta con N2 en la región central. No se observan
interferencias constructivas a ángulos altos, es decir cuando nos alejamos del
centro del patrón.
Si la disposición bidimensional es regular se puede
considerar como una disposición de rendijas alineadas. El patrón obtenido es la
suma de los patrones de difracción de conjuntos de rendijas. La intensidad del
máximo central depende de los difractores y de la potencia del emisor. Se
obtiene interferencia a altos ángulos.
Las redes tridimensionales revelan patrones de Fraunhofer
de interferencia tridimensional. Los sólidos cristalinos son redes de
difracción tridimensionales.
A cada red le corresponde una radiación de longitud de onda
(l) adecuada. Los rayos-X tienen longitudes de onda en el rango de unos pocos
Å( 10-10 m) y los sólidos cristalinos son distribuciones moleculares con una
periodicidad de Å.
El experimento de Laue en 1912 obtuvo un patrón de
Fraunhofer tridimensional utilizando como red de difracción un cristal para la
radiación de rayos-X y obteniendo máximos de difracción que responden a 2dsen m
θ λ = donde d son las distancias entre planos del cristal.








No hay comentarios:
Publicar un comentario